MOVIMIENTO
MOVIMIENTO RECTILÍNEO UNIFORME
Un movimiento es rectilíneo cuando un móvil describe una trayectoria recta, y es uniforme cuando su velocidad es constante en el tiempo, dado que su aceleración es nula. Nos referimos a él mediante el acrónimo MRU.
- Movimiento que se realiza sobre una línea recta.
- Velocidad constante; implica magnitud y dirección constantes.
- La magnitud de la velocidad recibe el nombre de celeridad o rapidez.
- Aceleración nula.
La distancia recorrida se calcula multiplicando la magnitud de la velocidad o rapidez por el tiempo transcurrido. Esta relación también es aplicable si la trayectoria no es rectilínea, con tal que la rapidez o módulo de la velocidad sea constante.
Por lo tanto el movimiento puede considerarse en dos sentidos; una velocidad negativa representa un movimiento en dirección contraria al sentido que convencionalmente hayamos adoptado como positivo.
De acuerdo con la Primera Ley de Newton, toda partícula permanece en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza externa que actúe sobre el cuerpo, dado que las fuerzas actuales están en equilibrio, por lo cual su estado es de reposo o de movimiento rectilíneo uniforme. Esta es una situación ideal, ya que siempre existen fuerzas que tienden a alterar el movimiento de las partículas, por lo que en el movimiento rectilíneo uniforme (M.R.U) es difícil encontrar la fuerza amplificada.
MOVIMIENTO RECTILÍNEO UNIFORME ACELERADO
El movimiento rectilíneo uniformemente acelerado (MRUA), también conocido como movimiento rectilíneo uniformemente variado (MRUV), es aquel en el que un movil se desplaza sobre una trayectoria recta estando sometido a una aceleración constante.
Un ejemplo de este tipo de movimiento es el de caída libre vertical, en el cual la aceleración interviniente, y considerada constante, es la que corresponde a la gravedad.
También puede definirse como el movimiento que realiza una partícula que partiendo del reposo es acelerada por una fuerza constante.
El movimiento rectilíneo uniformemente acelerado (MRUA) es un caso particular del movimiento uniformemente acelerado(MUA).
Este es el significado del movimiento uniformemente acelerado, el cual “en tiempos iguales, adquiere iguales incrementos de rapidez”.
En este tipo de movimiento sobre la partícula u objeto actúa una fuerza que puede ser externa o interna.
En este movimiento la velocidad es variable, nunca permanece constante; lo que si es constante es la aceleración.
Entenderemos como aceleración la variación de la velocidad con respecto al tiempo. Pudiendo ser este cambio en la magnitud(rapidez), en la dirección o en ambos.
Las variables que entran en juego (con sus respectivas unidades de medida) al estudiar este tipo de movimiento son:
Velocidad inicial Vo (m/s)
Velocidad final Vf (m/s)
Aceleración a (m/s2)
Tiempo t (s)
Distancia d (m)
TIRO VERTICAL
Es un movimiento sujeto a la aceleración gravitacional, solo que ahora es la aceleración la que se opone al movimiento inicial del objeto. El tiro vertical comprende subida y bajada de los cuerpos u objetos.
CARACTERÍSTICAS:
Nunca la velocidad inicial es cero.
Cuando el objeto alcance su altura máxima su velocidad en este punto es cero, mientras el objeto está de subida el signo de la velocidad es positivo y la velocidad es cero en su altura máxima, cuando comienza el descenso el signo de la velocidad es negativo.
La velocidad de subida es igual a la de bajada pero el signo de la velocidad al descender es negativo.
CARACTERÍSTICAS:
Nunca la velocidad inicial es cero.
Cuando el objeto alcance su altura máxima su velocidad en este punto es cero, mientras el objeto está de subida el signo de la velocidad es positivo y la velocidad es cero en su altura máxima, cuando comienza el descenso el signo de la velocidad es negativo.
La velocidad de subida es igual a la de bajada pero el signo de la velocidad al descender es negativo.
CAÍDA LIBRE
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo es frecuente también referirse coloquial mente a éstas como caídas libres, aunque los efectos de la viscosidad del medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción des aceleradora de la gravedad, como un disparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentación alar ni de paracaídas durante un cierto trayecto.
Si el movimiento considerado es de descenso o de caída, el valor de g resulta positivo como corresponde a una auténtica aceleración. Si, por el contrario, es de ascenso en vertical el valor deg se considera negativo, pues se trata, en tal caso, de un movimiento decelerado.
Para resolver problemas con movimiento de caída libre utilizamos las siguientes fórmulas:
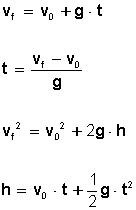
MOVIMIENTO DE PROYECTILES
Cuando un objeto es lanzado al aire, éste sufre una aceleración debida al efecto del campo gravitacional.
El movimiento más sencillo de éste tipo es la caída libre; pero cuando un cuerpo, además de desplazarse verticalmente, se desplaza horizontalmente, se dice que tiene un movimiento de proyectil, también conocido como movimiento parabólico, que es un caso más general de un cuerpo que se lanza libremente al campo gravitacional, y se trata de un movimientobidimensional.
Un objeto que se lanza al espacio sin fuerza de propulsión propia recibe el nombre de proyectil*.
En éste movimiento, se desprecia el efecto de la resistencia del aire; entonces, el único efecto que un proyectil sufre en su movimiento es su peso, lo que le produce una aceleración constante igual al valor de la gravedad.

Si la aceleración la definimos como una cantidad vectorial, entonces debería tener componentes en x e y. Pero para el caso, la única aceleración existente en el movimiento es la de la gravedad; como no existe ningún efecto en el movimiento horizontal del proyectil, la aceleración no tiene componente en x, y se limita entonces a ser un vector con dirección en el eje y.
Con lo anterior no quiere decir que la componente en x de la velocidad sea igual a cero (recordando que la velocidad es un vector).
Al analizar el movimiento en el eje x, la aceleración es igual a cero, entonces no existe cambio de la velocidad en el tiempo; por lo tanto, en el eje x se da un movimiento rectilíneo uniforme (M.R.U.).
Cuando el movimiento del proyectil es completo, es decir, se forma la parábola como se muestra en la figura anterior, el desplazamiento máximo en x (Xmax) se le conoce como elalcance horizontal del movimiento.
En cambio, en el eje y, se tiene una aceleración constante, igual al valor de la gravedad. Como la aceleración es constante, en el eje y se tiene un movimiento igual a una caída libre de un cuerpo.
Cuando el movimiento del proyectil forma la parábola que se muestra en la figura anterior, el desplazamiento máximo en y (Ymax) se conoce como la altura máxima del movimiento.
Si el movimiento es completo (forma la parábola completa), la altura máxima se da justamente en la mitad del tiempo en el que se llega al alcance horizontal; es decir, a la mitad del tiempo del movimiento completo.
La forma más sencilla de resolver problemas que involucran éste tipo de movimiento es analizar el movimiento en cada eje, encontrando las componentes de la velocidad en cada eje y sus desplazamientos.
Las fórmulas que se utilizan son las mismas deducidas para el M.R.U. y la caída libre.
MOVIMIENTO CIRCULAR UNIFORME
En física, el movimiento circular uniforme (también denominado movimiento uniformemente circular) describe el movimiento de un cuerpo atravesando, con rapidez constante, una trayectoria circular.
Aunque la rapidez del objeto es constante, su velocidad no lo es: La velocidad, una magnitud vectorial, tangente a la trayectoria, en cada instante cambia de dirección. Esta circunstancia implica la existencia de una aceleración que, si bien en este caso no varía al módulo de la velocidad, sí varía su dirección.
Estamos rodeados por objetos que describen movimientos circulares: un disco compacto durante su reproducción en el equipo de música, las manecillas de un reloj o las ruedas de una motocicleta son ejemplos de movimientos circulares; es decir, de cuerpos que se mueven describiendo una circunferencia.
A veces el movimiento circular no es completo: cuando un coche o cualquier otro vehículo toma una curva realiza un movimiento circular, aunque nunca gira los 360º de la circunferencia.
La experiencia nos dice que todo aquello da vueltas tiene movimiento circular. Si lo que gira da siempre el mismo número de vueltas por segundo, decimos que posee movimiento circular uniforme (MCU).
Ejemplos de cosas que se mueven con movimiento circular uniforme hay muchos:
La tierra es uno de ellos. Siempre da una vuelta sobre su eje cada 24 horas. También gira alrededor del sol y da una vuelta cada 365 días. Un ventilador, un lavarropas o los viejos tocadiscos, la rueda de un auto que viaja con velocidad constante, son otros tantos ejemplos.
MOVIMIENTO CIRCULAR UNIFORMEMENTE ECELERADO
El Movimiento circular uniformemente acelerado (MCUA), es un movimiento circular cuya aceleración α es constante. Es un caso particular de la velocidad y la aceleración angular.
Dada la aceleración angular α podemos obtener el incremento de la velocidad angular ω entre los instantes t0 y t1. La ecuación resultante de la velocidad es:
- ω (t)=ω0+α0(t1-t0)
Siendo α la aceleración, ω0 la velocidad inicial, y (t1-t0) el incremento de tiempo.
Dada la velocidad angular ω en función del tiempo, podemos hallar la posición θ entre los instantes t0 y t1. La ecuación resultante es:
- Δθ=ω0·Δt +½a0·(Δt)²
- ω²=ω²0+2αΔθ
Siendo a0 la aceleración, ω0 la velocidad inicial, y (t1-t0) el incremento de tiempo.
Apréciese la similitud con las fórmulas del MRUA, movimiento rectilíneo uniformemente acelerado.
Cuando durante el movimiento circular de un móvil su velocidad no permanece constante, sino que varía decimos que sufre una aceleración angular. Cuando la velocidad angular varía es conveniente determinar cuál su aceleración angular media, misma que se expresa de la siguiente manera: ififmtt−−=ωωα
Aceleración angular instantánea
Cuando en el móvil acelerado de un cuerpo que sigue una trayectoria circular, los intervalos de tiempo considerados son cada vez más pequeños, la aceleración angular media se aproxima a una aceleración angular instantánea.
Cuando el intervalo de tiempo es muy pequeño que tiende a cero, la aceleración del cuerpo es instantánea.
Analogías entre el movimiento lineal y circular
Lineal Circular
d (m) θ (rad)
V (m/s) ω (rad/s)
a (m/s2)α (rad/s2)
Ecuaciones que relacionan al movimiento lineal y circular
d = θ r
V = ω r
a = α r
Unidades
d =distancia de arco =cm, m
θ =desplazamiento angular =rad
r =radio =cm, =m
V =velocidad lineal =cm/s, m/s
ω =velocidad angular =rad/s
a =aceleración lineal =cm/s2, m/s2
α =aceleración angular =rad/s2
FUERZA
LEYES DE NEWTON
La primera ley de Newton, conocida también como Ley de inercía, nos dice que si sobre un cuerpo no actua ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero).
Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actua ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
La Fuerza que actua sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
Otra consecuencia de expresar la Segunda ley de Newton usando la cantidad de movimiento es lo que se conoce como Principio de conservación de la cantidad de movimiento. Si la fuerza total que actua sobre un cuerpo es cero, la Segunda ley de Newton nos dice que:
Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos.
De modo más simple:
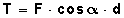
Donde m es la masa del objeto, g es la aceleración de gravedad y h es la altura del objeto. Así que según la pelota cae, su energía potencial disminuye por virtud de la reducción en la altura.
Podemos definir la energía total de la pelotaa como la suma de la energía cinética y la potencial.
Como la energía permanece constante, entonces la energía total inicial es igual a la energía total final.
Por lo que entonces la suma de la energía cinética inicial y la potencial inicial debe ser igual a la suma de la energía cinética final y la energía potencial final.
o sea
Considera un ciclista que intenta subir una cuesta sólo con el impulso. Según el ciclista sube la cuesta, su velocidad irá disminuyendo, por lo que la energía cinética disminuirá. La razón es que el trabajo realizado por la fuerza de gravedad en este caso es negativo debido a que el desplazamiento es hacia la parte alta del plano, mientras que el componente de la fuerza de gravedad que actúa en el ciclista es hacia la parte baja del plano. Esta pérdida en energía cinética se compensa con un aumento en la energía potencial. La altura aumentará hasta alcanzar aquella altura que le da una energía potencial igual a la energía cinética del ciclista justo antes de comenzar a subir la cuesta. Mientras más rápido vaya el ciclista al momento de comenzar a subir la cuesta, más alto subirá.
Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el interventor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el interventor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actua ninguna fuerza neta se mueve con velocidad constante.
En realidad, es imposible encontrar un sistema de referencia inercial, puesto que siempre hay algún tipo de fuerzas actuando sobre los cuerpos, pero siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial. En muchos casos, suponer a un observador fijo en la Tierra es una buena aproximación de sistema inercial.
La Primera ley de Newton nos dice que para que un cuerpo altere su movimiento es necesario que exista algo que provoque dicho cambio. Ese algo es lo que conocemos como fuerzas. Estas son el resultado de la acción de unos cuerpos sobre otros.
La Segunda ley de Newton se encarga de cuantificar el concepto de fuerza. Nos dice que la fuerza neta aplicada sobre un cuerpo es proporcional a la aceleración que adquiere dicho cuerpo. La constante de proporcionalidad es la masa del cuerpo, de manera que podemos expresar la relación de la siguiente manera:
F = m a
Tanto la fuerza como la aceleración son magnitudes vectoriales, es decir, tienen, además de un valor, una dirección y un sentido. De esta manera, la Segunda ley de Newton debe expresarse como:
F = m a
La unidad de fuerza en el Sistema Internacional es el Newton y se representa por N. Un Newton es la fuerza que hay que ejercer sobre un cuerpo de un kilogramo de masa para que adquiera una aceleración de 1 m/s2, o sea,
1 N = 1 Kg · 1 m/s2
La expresión de la Segunda ley de Newton que hemos dado es válida para cuerpos cuya masa sea constante. Si la masa varia, como por ejemplo un cohete que va quemando combustible, no es válida la relación F = m ·a. Vamos a generalizar la Segunda ley de Newton para que incluya el caso de sistemas en los que pueda variar la masa.Para ello primero vamos a definir una magnitud física nueva. Esta magnitud física es la cantidad de movimiento que se representa por la letra p y que se define como el producto de la masa de un cuerpo por su velocidad, es decir:
p = m · v
La cantidad de movimiento también se conoce como momento lineal. Es una magnitud vectorial y, en el Sistema Internacional se mide en Kg·m/s . En términos de esta nueva magnitud física, la Segunda ley de Newton se expresa de la siguiente manera:La Fuerza que actua sobre un cuerpo es igual a la variación temporal de la cantidad de movimiento de dicho cuerpo, es decir,
F = dp/dt
De esta forma incluimos también el caso de cuerpos cuya masa no sea constante. Para el caso de que la masa sea constante, recordando la definición de cantidad de movimiento y que como se deriva un producto tenemos:
F = d(m·v)/dt = m·dv/dt + dm/dt ·v
Como la masa es constante
dm/dt = 0
y recordando la definición de aceleración, nos queda
F = m a
tal y como habiamos visto anteriormente.Otra consecuencia de expresar la Segunda ley de Newton usando la cantidad de movimiento es lo que se conoce como Principio de conservación de la cantidad de movimiento. Si la fuerza total que actua sobre un cuerpo es cero, la Segunda ley de Newton nos dice que:
0 = dp/dt
es decir, que la derivada de la cantidad de movimiento con respecto al tiempo es cero. Esto significa que la cantidad de movimiento debe ser constante en el tiempo (la derivada de una constante es cero). Esto es elPrincipio de conservación de la cantidad de movimiento: si la fuerza total que actua sobre un cuerpo es nula, la cantidad de movimiento del cuerpo permanece constante en el tiempo.Tal como comentamos en al principio de la Segunda ley de Newton las fuerzas son el resultado de la acción de unos cuerpos sobre otros.
La tercera ley, también conocida como Principio de acción y reacción nos dice que si un cuerpo A ejerce una acción sobre otro cuerpo B, éste realiza sobre A otra acción igual y de sentido contrario.
Esto es algo que podemos comprobar a diario en numerosas ocasiones. Por ejemplo, cuando queremos dar un salto hacia arriba, empujamos el suelo para impulsarnos. La reacción del suelo es la que nos hace saltar hacia arriba.
Cuando estamos en una piscina y empujamos a alguien, nosotros tambien nos movemos en sentido contrario. Esto se debe a la reacción que la otra persona hace sobre nosotros, aunque no haga el intento de empujarnos a nosotros.
Hay que destacar que, aunque los pares de acción y reacción tenga el mismo valor y sentidos contrarios, no se anulan entre si, puesto que actuan sobre cuerpos distintos.
EQUILIBRIO TRASLACIONAL
Un cuerpo se encuentra en equilibrio traslacional cuando la sumatoria de todas las componentes en X es igual a 0 y todas las componentes en Y es igual a 0.
Cuando un cuerpo esta en equilibrio traslacional no tiene fuerza resultante actuando sobre el.
| |
|
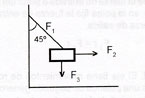
Una caja de 8 N está suspendida por un alambre de 2 m que forma un ángulo de 45° con la vertical. ¿Cuál es el valor de las fuerzas horizontal y en el alambre para que el cuerpo se mantenga estático?.
Primero se visualiza el problema de la siguiente manera:
Primero se visualiza el problema de la siguiente manera:

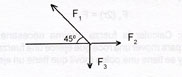
A continuación se elabora su diagrama de cuerpo libre.

Ahora por medio de la descomposición de los vectores, calculamos la fuerza de cada uno de ellos.
F1x = - F1 cos 45°*
F1y = F1 sen 45°
F2x = F2 cos 0° = F2
F2y = F2sen0°=0
F3x = F3cos90°=0
F3y = - F3 sen 90° = - 8 N*
F1y = F1 sen 45°
F2x = F2 cos 0° = F2
F2y = F2sen0°=0
F3x = F3cos90°=0
F3y = - F3 sen 90° = - 8 N*
Porque los cuadrantes en los que se localizan son negativos.
Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos losiguiente:
Como únicamente conocemos los valores de F3, F2 y la sumatoria debe ser igual a cero en x e y, tenemos losiguiente:
EFx=F1x+F2x+F3x=0
EFy=F1y+F2y+F3y=0
Por lo tanto tenemos lo siguiente:
EFx=-F1 cos 45+F2=0
F2=F1(0.7071)
EFy=-F1sen45-8N=0
8N=F1(0.7071)
F1=8N/0.7071=11.31 N
F2=F1(0.7071)
EFy=-F1sen45-8N=0
8N=F1(0.7071)
F1=8N/0.7071=11.31 N
Para calcular F2, se sustituye F1 de la ecuación siguiente:
F2=F1(0.7071)
F2=11.31(0.7071)=8N
F2=11.31(0.7071)=8N
EQUILIBRIO ROTACIONAL
Es aquel equilibrio que ocurre cuando un cuerpo sufre un movimiento de rotacion o giro, al igual que el equilibrio traslacional debe tambien equilibrarse; surge en el momento en que todas las torcas que actúan sobre el cuerpo sean nulas, o sea, la sumatoria de las mismas sea igual a cero.
EMx= 0
EMy= 0
su fuerza se mide en torques o torcas es una magnitud (pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza.Explicado de una forma mas sencilla el torque es el producto entre la fuerza aplicada y la distancia a la cual se la aplica medida, generalmente, desde el punto que permanece fijo.
Así como una fuerza provoca una traslación, un torque produce una rotación.
El torque mide, de alguna manera, el estado de rotación que provoca la fuerza o la tendencia a producir una rotación.Del mismo modo que puede evitarse el desplazamiento de un objeto aplicando una fuerza contraria a la que lo hace mover, puede evitarse una rotación aplicando un torque contrario al que lo hace girar.
Ejemplos de rotacion y su fuerzas aplicadas


CONDICION DE EQUILIBRIO DE ROTACIÓN
Si a un cuerpo que puede girar alrededor de un eje, se la aplican varias fuerzas y no producen variación en su movimiento de rotación, se dice que el cuerpo puede estar en reposo o tener movimiento uniforme de rotación.
Para que exista este equilibrio se presentan los siguientes factores
a) Par de fuerzas: Se produce un par de fuerzas cuando dos fuerzas paralelas de la misma magnitud pero en sentido contrario actuan sobre un cuerpo, su resultante es igual a cero y su aplicacion esta en el centro de la linea que une los puntos de inicio de las fuerzas componentes.
b) Momento de una fuerza: Llamado tambien momento de torsion o torque y se define como la capacidad que tiene una fuerza para hacer girar un cuerpo, es decir es la intensidad con que una fuerza tiende a comunicarle un movimiento de rotacion. El momento de una fuerza se obtiene multiplicando el valor de la fuerza por su brazo de palanca.
c)Centro de gravedad.
El centro de gravedad (CG) es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas masas materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo (dicho punto no necesariamente corresponde a un punto material del cuerpo, ya que puede estar situado fuera de él.
d)Equilibrio estático: existe un equilibrio estático cuando todas las fuerzas que actúan
sobre todos los componentes de un sistema están equilibradas.
e)Vectores: un vector es una magnitud que tiene dos características: módulo, o magnitud,
y dirección. Los vectores normalmente se dibujan como flechas. Una fuerza y el
momento de una fuerza son magnitudes vectoriales
Aplicaciones de el equilibrio rotacional
El equilibrio rotacional se puede aplicar en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.
EMx= 0
EMy= 0
su fuerza se mide en torques o torcas es una magnitud (pseudo)vectorial, obtenida como producto vectorial del vector de posición del punto de aplicación de la fuerza con respecto al punto al cual se toma el momento por la fuerza.Explicado de una forma mas sencilla el torque es el producto entre la fuerza aplicada y la distancia a la cual se la aplica medida, generalmente, desde el punto que permanece fijo.
Así como una fuerza provoca una traslación, un torque produce una rotación.
El torque mide, de alguna manera, el estado de rotación que provoca la fuerza o la tendencia a producir una rotación.Del mismo modo que puede evitarse el desplazamiento de un objeto aplicando una fuerza contraria a la que lo hace mover, puede evitarse una rotación aplicando un torque contrario al que lo hace girar.
Ejemplos de rotacion y su fuerzas aplicadas


CONDICION DE EQUILIBRIO DE ROTACIÓN
Si a un cuerpo que puede girar alrededor de un eje, se la aplican varias fuerzas y no producen variación en su movimiento de rotación, se dice que el cuerpo puede estar en reposo o tener movimiento uniforme de rotación.
Para que exista este equilibrio se presentan los siguientes factores
a) Par de fuerzas: Se produce un par de fuerzas cuando dos fuerzas paralelas de la misma magnitud pero en sentido contrario actuan sobre un cuerpo, su resultante es igual a cero y su aplicacion esta en el centro de la linea que une los puntos de inicio de las fuerzas componentes.
b) Momento de una fuerza: Llamado tambien momento de torsion o torque y se define como la capacidad que tiene una fuerza para hacer girar un cuerpo, es decir es la intensidad con que una fuerza tiende a comunicarle un movimiento de rotacion. El momento de una fuerza se obtiene multiplicando el valor de la fuerza por su brazo de palanca.
c)Centro de gravedad.
El centro de gravedad (CG) es el punto de aplicación de la resultante de todas las fuerzas de gravedad que actúan sobre las distintas masas materiales de un cuerpo, de tal forma que el momento respecto a cualquier punto de esta resultante aplicada en el centro de gravedad es el mismo que el producido por los pesos de todas las masas materiales que constituyen dicho cuerpo. En otras palabras, el centro de gravedad de un cuerpo es el punto respecto al cual las fuerzas que la gravedad ejerce sobre los diferentes puntos materiales que constituyen el cuerpo producen un momento resultante nulo (dicho punto no necesariamente corresponde a un punto material del cuerpo, ya que puede estar situado fuera de él.
d)Equilibrio estático: existe un equilibrio estático cuando todas las fuerzas que actúan
sobre todos los componentes de un sistema están equilibradas.
e)Vectores: un vector es una magnitud que tiene dos características: módulo, o magnitud,
y dirección. Los vectores normalmente se dibujan como flechas. Una fuerza y el
momento de una fuerza son magnitudes vectoriales
Aplicaciones de el equilibrio rotacional
El equilibrio rotacional se puede aplicar en todo tipo de instrumentos en los cuales se requiera aplicar una o varias fuerzas o torques para llevar a cabo el equilibrio de un cuerpo. Entre los instrumentos más comunes están la palanca,la balanza romana, la polea, el engrane, etc.
FRICCIÓN
La fricción es una fuerza de contacto que actúa para oponerse al movimiento deslizante entre superficies. Actúa paralela a la superficie y opuesta al sentido del deslizamiento. Se denomina como Ff . La fuerza de fricción también se le conoce como fuerza de rozamiento.
La fricción ocurre cuando dos objetos se deslizan entre sí o tienden a deslizarse. Cuando un cuerpo se mueve sobre una superficie o a través de un medio viscoso, como el aire o el agua, hay una resistencia al movimiento debido a que el cuerpo interactúa con sus alrededores. Dicha resistencia recibe también el nombre de fricción. Podemos observar el siguiente ejemplo:
Observa que el hombre realiza una fuerza sobre el objeto a la cual llamamos fuerza de empuje, también podemos llamarle fuerza aplicada. Podemos asumir que el objeto se desliza a la derecha, sin que haya rotación. La dirección de la fuerza, también es a la derecha, mientras que la fricción se dirige a la izquierda. En otras palabras la fuerza de fricción actúa paralela a la superficie y en contra del movimiento.
La forma general de escribir la ecuación para la fuerza de fricción es de la siguiente manera:
donde Ff es la fuerza de fricción mientras que μ es el coeficiente de fricción
Fricción estática
Ff=μsFN
Fricción cinética
Ff=μkFN
TRABAJO
Como idea general, hablamos de trabajo cuando una fuerza (expresada en newton) mueve un cuerpo y libera la energía potencialde este; es decir, un hombre o una maquina realiza un trabajo cuando vence una resistencia a lo largo de un camino.
Por ejemplo, para levantar una caja hay que vencer una resistencia, el peso P del objeto, a lo largo de un camino, la altura d a la que se levanta la caja. El trabajo T realizado es el producto de la fuerza P por la distancia recorrida d.
T = F · d Trabajo = Fuerza • Distancia
Aquí debemos hacer una aclaración.
Como vemos, y según la fórmula precedente, Trabajo es el producto (la multiplicación) de la distancia (d) (el desplazamiento) recorrida por un cuerpo por el valor de la fuerza (F) aplicada en esa distancia y es una magnitud escalar, que también se expresa enJoule (igual que la energía).
De modo más simple:
 |
| Este trabajo también equivale a la fuerza por la distancia. |
La unidad de trabajo (en Joule) se obtiene multiplicando la unidad de fuerza (en Newton) por la unidad de longitud (en metro).
Recordemos que el newton es la unidad de fuerza del Sistema Internacional (SI) que equivale a la fuerza necesaria para que un cuerpo de 1 kilogramo masa adquiera una aceleración de un metro por segundo cada segundo (lo mismo que decir “por segundo al cuadrado”). Su símbolo es N.
Por lo tanto, 1 joule es el trabajo realizado por una fuerza de 1 Newton al desplazar un objeto, en la dirección de la fuerza, a lo largo de 1 metro.
Aparece aquí la expresión “dirección de la fuerza” la cual puede ser horizontal. oblicua o vertical respecto a la dirección en que se mueve el objeto sobre el cual se aplica la fuerza.
En tal sentido, la “dirección de la fuerza” y la “dirección del movimiento” pueden formar un ángulo (o no formarlo si ambas son paralelas).
Si forman un ángulo (α), debemos incorporar ese dato en nuestra fórmula para calcular el trabajo, para quedar así:
Lo cual se lee: Trabajo = fuerza por coseno de alfa por distancia
OJO: El valor del coseno lo obtenemos usando la calculadora.
Si el ángulo es recto (90º) el coseno es igual a cero (0).
Si el ángulo es Cero (fuerza y movimiento son paralelos) el coseno es igual a Uno (1).
Nota:
En la fórmula para calcular el trabajo, algunos usan la letra W en lugar de T.
Así: W = F • cosα • d
Energía cinética final
Una variante para calcular el trabajo la tenemos cuando conocemos la Energía cinética final (Ecf) y conocemos la Energía cinética inicial (Eci) utilizando el Teorema trabajo-energía, expresado en la fórmula:
T = ½m vf2 –½m vi2 = Ecf – Eci = ΔEc (variación de energía cinética)
Que simplificada queda
T = Ecf – Eci
T = trabajo entre la posición final y la posición inicial
Ecf = energía cinética final
Eci = energía cinética inicial
Ecf = energía cinética final
Eci = energía cinética inicial
Usando esta fórmula, si conocemos el trabajo realizado y tenemos una de las energías cinéticas, se puede calcular la otra energía cinética.
Cuando la rapidez es constante, no hay variación de energía cinética y el trabajo de la fuerza neta es cero.
POTENCIA
En la vida cotidiana, interesa saber no sólo el trabajo que se pueda efectuar, sino también la rapidez con que se realiza.
Una persona está limitada en el trabajo que pueda efectuar, no sólo por la energía total necesaria, sino también por la rapidez con que transforma esa energía.
Se define potencia como la rapidez a la cual se efectúa trabajo, o bien, como la rapidez de transferencia de energía en el tiempo.
Potencia = W/t = trabajo/tiempo = energía transformada/tiempo.
En el Sistema Internacional la potencia se expresa en
Joules por segundo, unidad a la que se le da el nombre
Watt (W), 1 W = 1J/s.
Joules por segundo, unidad a la que se le da el nombre
Watt (W), 1 W = 1J/s.
Cuando decimos que una ampolleta consume 60 watts, estamos diciendo que transforma en cada segundo 60 Joules de energía eléctrica en energía luminosa o térmica.
Para potencias elevadas se usa el caballo de fuerza, abreviado hp, que equivale a 746 Watts.
1 hp = 746 watts
A veces conviene expresar la potencia en términos de la fuerza neta F aplicada a un objeto y de su velocidad.
P = W/t. P = W/t. Como W = Fuerza (F) * desplazamiento (x) = Fx, P = Fx/t.
Si la velocidad v es constante, v = x/t obteniendo,
 P = Fv, esto es, fuerza por velocidad.
P = Fv, esto es, fuerza por velocidad.
Si la velocidad v es constante, v = x/t obteniendo,
Si la velocidad v es variable se usa la potencia instantánea definida como
 P = dW/dt
P = dW/dt  donde p es el símolo de derivada.
donde p es el símolo de derivada.
O sea la potencia instantánea es el trabajo por unidad de tiempo durante un pequeñísimo intervalo de tiempo dt.
Como dW = Fdx y v = dx/dt resulta


 P = Fv
P = Fv
esto es, fuerza por velocidad instantánea.
O sea la potencia instantánea es el trabajo por unidad de tiempo durante un pequeñísimo intervalo de tiempo dt.
Como dW = Fdx y v = dx/dt resulta
esto es, fuerza por velocidad instantánea.
ENERGÍA POTENCIAL
La energía potencial es el tipo de energía mecánica asociada a la posición o configuración de un objeto. Podemos pensar en la energía potencial como la energía almacenada en el objeto debido a su posición y que se puede transformar en energía cinética o trabajo. El concepto energía potencial, U, se asocia con las llamadas fuerzas conservadoras. Cuando una fuerza conservadora, como la fuerza de gravedad, actúa en un sistema u objeto; la energía cinética ganada (o perdida) por el sistema es compensada por una perdida (o ganancia) de una cantidad igual de energía potencial. Esto ocurre según los elementos del sistema u objeto cambia de posición.
Una fuerza es conservadora si el trabajo realizado por ésta en un objeto es independiente de la ruta que sigue el objeto en su desplazamiento entre dos puntos. Otras fuerzas conservadoras son: la fuerza electrostática y la fuerza de restauración de un resorte.
Considera una pelota cayendo. La fuerza de gravedad realiza trabajo en la pelota. Como la dirección de la fuerza de gravedad es dirección del desplazamiento de la pelota, el trabajo realizado por la gravedad es positivo. El que el trabajo sea positivo significa que la energía cinética aumentará según la pelota cae. Es decir, la velocidad de la pelota aumentará.
Según la energía cinética aumenta, la ganancia debe ser compensada por una perdida de una cantidad igual en energía potencial. Es decir, según la pelota cae, la energía cinética aumenta mientras que la energía potencial disminuye.
Se define la energía potencial como:
Una fuerza es conservadora si el trabajo realizado por ésta en un objeto es independiente de la ruta que sigue el objeto en su desplazamiento entre dos puntos. Otras fuerzas conservadoras son: la fuerza electrostática y la fuerza de restauración de un resorte.
Considera una pelota cayendo. La fuerza de gravedad realiza trabajo en la pelota. Como la dirección de la fuerza de gravedad es dirección del desplazamiento de la pelota, el trabajo realizado por la gravedad es positivo. El que el trabajo sea positivo significa que la energía cinética aumentará según la pelota cae. Es decir, la velocidad de la pelota aumentará.
Según la energía cinética aumenta, la ganancia debe ser compensada por una perdida de una cantidad igual en energía potencial. Es decir, según la pelota cae, la energía cinética aumenta mientras que la energía potencial disminuye.
Se define la energía potencial como:
U = mgh
Donde m es la masa del objeto, g es la aceleración de gravedad y h es la altura del objeto. Así que según la pelota cae, su energía potencial disminuye por virtud de la reducción en la altura.
Podemos definir la energía total de la pelotaa como la suma de la energía cinética y la potencial.
ET = K + U
Como la energía permanece constante, entonces la energía total inicial es igual a la energía total final.
ETi = ETf
Por lo que entonces la suma de la energía cinética inicial y la potencial inicial debe ser igual a la suma de la energía cinética final y la energía potencial final.
Ki + Ui = Kf + Uf
o sea
½ mvi² + mghi = ½ mvf² + mghf
Considera un ciclista que intenta subir una cuesta sólo con el impulso. Según el ciclista sube la cuesta, su velocidad irá disminuyendo, por lo que la energía cinética disminuirá. La razón es que el trabajo realizado por la fuerza de gravedad en este caso es negativo debido a que el desplazamiento es hacia la parte alta del plano, mientras que el componente de la fuerza de gravedad que actúa en el ciclista es hacia la parte baja del plano. Esta pérdida en energía cinética se compensa con un aumento en la energía potencial. La altura aumentará hasta alcanzar aquella altura que le da una energía potencial igual a la energía cinética del ciclista justo antes de comenzar a subir la cuesta. Mientras más rápido vaya el ciclista al momento de comenzar a subir la cuesta, más alto subirá.
ENERGÍA CINÉTICA
Cuando un cuerpo está en movimiento posee energía cinética ya que al chocar contra otro puede moverlo y, por lo tanto, producir un trabajo.
Para que un cuerpo adquiera energía cinética o de movimiento; es decir, para ponerlo en movimiento, es necesario aplicarle una fuerza. Cuanto mayor sea el tiempo que esté actuando dicha fuerza, mayor será la velocidad del cuerpo y, por lo tanto, su energía cinética será también mayor.
Otro factor que influye en la energía cinética es la masa del cuerpo.
Por ejemplo, si una bolita de vidrio de 5 gramos de masa avanza hacia nosotros a una velocidad de 2 km / h no se hará ningún esfuerzo por esquivarla. Sin embargo, si con esa misma velocidad avanza hacia nosotros un camión, no se podrá evitar la colisión.
La fórmula que representa la Energía Cinética es la siguiente:
E c = 1 / 2 • m • v 2
|
E c = Energía cinética
m = masa
v = velocidad
Cuando un cuerpo de masa m se mueve con una velocidad v posee una energía cinética que está dada por la fórmula escrita más arriba.
En esta ecuación, debe haber concordancia entre las unidades empleadas. Todas ellas deben pertenecer al mismo sistema. En el Sistema Internacional (SI), la masa m se mide en kilogramo (kg) y la velocidad v en metros partido por segundo ( m / s), con lo cual la energía cinética resulta medida en Joule ( J ).






.jpg)

.jpg)

.jpg)
.jpg)










.jpg)


.jpg)
No hay comentarios:
Publicar un comentario